Full Adder (Logic): Difference between revisions
From TernaryWiki
Jump to navigationJump to search
mNo edit summary |
No edit summary |
||
| Line 8: | Line 8: | ||
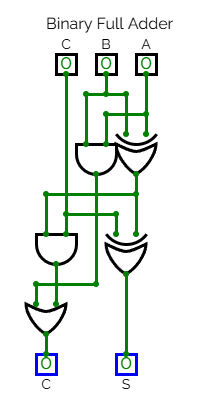
<div style="display: inline-block;">[[File:Full_Adder_Binary.png|frame|none|alt=Logic gate layout for a binary full adder.|Binary Full Adder]]</div> | <div style="display: inline-block;">[[File:Full_Adder_Binary.png|frame|none|alt=Logic gate layout for a binary full adder.|Binary Full Adder]]</div> | ||
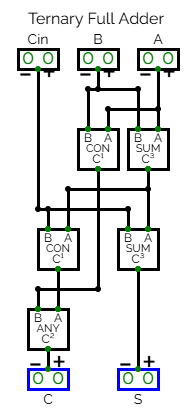
<div style="display: inline-block;">[[File:Full_Adder_Ternary.png|frame|none|alt=BCT logic gate layout for a ternary full adder.|Ternary Full Adder]]</div> | <div style="display: inline-block;">[[File:Full_Adder_Ternary.png|frame|none|alt=BCT logic gate layout for a ternary full adder.|Ternary Full Adder]]</div> | ||
</div> | |||
== Truth Tables == | |||
<div class="tt"> | |||
<table class="tt"> | |||
<tr> | |||
<td class="tt_bb"><b>A</b></td> | |||
<td class="tt_bb"><b>B</b></td> | |||
<td class="tt_bb"><b>Ci</b></td> | |||
<td class="tt_bl tt_bb"><b>Co</b></td> | |||
<td class="tt_bb"><b>S</b></td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_r">-</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
<td class="tt_bl tt_g">0</td> | |||
<td class="tt_b">+</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_g">0</td> | |||
<td class="tt_bl tt_b">+</td> | |||
<td class="tt_r">-</td> | |||
</tr> | |||
<tr> | |||
<td class="tt_b">+</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_b">+</td> | |||
<td class="tt_bl tt_b">+</td> | |||
<td class="tt_g">0</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
Latest revision as of 19:57, 4 August 2025
An example where Binary and Ternary logic work the same is the Full and Half adder. The full adder layout is identical. The only difference is using each logic base's primary logic gates.
- XOR = SUM
- AND = CON
- OR = ANY
Truth Tables
| A | B | Ci | Co | S |
| - | - | - | - | 0 |
| - | - | 0 | - | + |
| - | - | + | 0 | - |
| - | 0 | - | - | + |
| - | 0 | 0 | 0 | - |
| - | 0 | + | 0 | 0 |
| - | + | - | 0 | - |
| - | + | 0 | 0 | 0 |
| - | + | + | 0 | + |
| 0 | - | - | - | + |
| 0 | - | 0 | 0 | - |
| 0 | - | + | 0 | 0 |
| 0 | 0 | - | 0 | - |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | + | 0 | + |
| 0 | + | - | 0 | 0 |
| 0 | + | 0 | 0 | + |
| 0 | + | + | + | - |
| + | - | - | 0 | - |
| + | - | 0 | 0 | 0 |
| + | - | + | 0 | + |
| + | 0 | - | 0 | 0 |
| + | 0 | 0 | 0 | + |
| + | 0 | + | + | - |
| + | + | - | 0 | + |
| + | + | 0 | + | - |
| + | + | + | + | 0 |